2017 September 10

一致性哈希表

摘要

这篇论文是一致性hash表的开山鼻祖。它使用在分布式网络中的缓存协议中，解决了网络中的hot spot热点问题。

简介

大型网络中经常遇到的几个问题是：

像这种中心化的CS服务模型，本论文所提供的工具方法都是适用的。

之前的工作

大多数使用proxy cache的方法来解决上面的两个问题，这种方法的基本原理就相当于数据库中的shared buffer的，其工作原理也基本是相同的。

有些论文使用了一组cache server来用作proxy cache。这种方法的缺点是，随着cache server数目的增长，管理这些cache server之间的缓存数据就成为了一个突出的问题。需要使用本论文中提出的一致性哈希来解决。

Harvest Cache也是一部分论文使用的方法，它大体使用的是树型方式来管理page cache的。这个方法的优点是分散了请求的压力，不会在短时间内形成高负载。缺点是，树的root节点在理论上是存在成为swamped的可能的。

Plaxton/Rajaraman算法则使用了随机+哈希的方法在多个cache中来平衡负载。这个算法存在的缺点同样也是swamped。

本论文的贡献

主要有两点：

  1. random cache trees, 结合了后两种论文中的方法；
  2. 一致性哈希，对已有哈希的加强，可以应对网络中机器的go up/down问题；

模型

browers <———> caches <———-> servers

目标主要有三个: 阻止swamped; 减少cache memory的大小； 降低获取页的延时；

一致性哈希

client和server之间有一层cache，用于减轻server的负载。那么，每一个cache只需要拥有其中的一部分数据。另外，client还需要知道向哪个cache去查询哪些数据对象。这个问题显示的方案是hash。server使用hash来把所有的对象分散到cache上去，而client使用hash来发现哪个cache缓存着数据对象。非一致性哈希有着灾难性的问题：所有数据得重分布； 之前的数据缓存全部作废了；

一致性哈希的几个属性：

定义

1、平衡性(Balance)：平衡性是指哈希的结果能够尽可能分布到所有的缓冲中去，这样可以使得所有的缓冲空间都得到利用。很多哈希算法都能够满足这一条件。

2、单调性(Monotonicity)：单调性是指如果已经有一些内容通过哈希分派到了相应的缓冲中，又有新的缓冲加入到系统中。哈希的结果应能够保证原有已分配的内容可以被映射到原有的或者新的缓冲中去，而不会被映射到旧的缓冲集合中的其他缓冲区。

3、分散性(Spread)：在分布式环境中，终端有可能看不到所有的缓冲，而是只能看到其中的一部分。当终端希望通过哈希过程将内容映射到缓冲上时，由于不同终端所见的缓冲范围有可能不同，从而导致哈希的结果不一致，最终的结果是相同的内容被不同的终端映射到不同的缓冲区中。这种情况显然是应该避免的，因为它导致相同内容被存储到不同缓冲中去，降低了系统存储的效率。分散性的定义就是上述情况发生的严重程度。好的哈希算法应能够尽量避免不一致的情况发生，也就是尽量降低分散性。

4、负载(Load)：负载问题实际上是从另一个角度看待分散性问题。既然不同的终端可能将相同的内容映射到不同的缓冲区中，那么对于一个特定的缓冲区而言，也可能被不同的用户映射为不同 的内容。与分散性一样，这种情况也是应当避免的，因此好的哈希算法应能够尽量降低缓冲的负荷。

构造

可以参考CSDN中的这篇文章 。以下大多数的内容都是来自于这篇文章，也是本论文理解之后所要表达的内容。

在分布式集群中，对机器的添加删除，或者机器故障后自动脱离集群这些操作是分布式集群管理最基本的功能。如果采用常用的hash(object)%N算法，那么在有机器添加或者删除后，很多原有的数据就无法找到了，这样严重的违反了单调性原则。接下来主要讲解一下一致性哈希算法是如何设计的：

环形Hash空间

按照常用的hash算法来将对应的key哈希到一个具有2^32次方个桶的空间中，即0~(2^32)-1的数字空间中。现在我们可以将这些数字头尾相连，想象成一个闭合的环形。如下图

把数据通过一定的hash算法处理后映射到环上

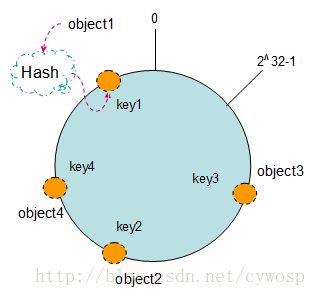
现在我们将object1、object2、object3、object4四个对象通过特定的Hash函数计算出对应的key值，然后散列到Hash环上。如下图：

    Hash(object1) = key1；

    Hash(object2) = key2；

    Hash(object3) = key3；

    Hash(object4) = key4

将机器通过hash算法映射到环上

在采用一致性哈希算法的分布式集群中将新的机器加入，其原理是通过使用与对象存储一样的Hash算法将机器也映射到环中（一般情况下对机器的hash计算是采用机器的IP或者机器唯一的别名作为输入值），然后以顺时针的方向计算，将所有对象存储到离自己最近的机器中。 假设现在有NODE1，NODE2，NODE3三台机器，通过Hash算法得到对应的KEY值，映射到环中，其示意图如下：

Hash(NODE1) = KEY1;
Hash(NODE2) = KEY2;
Hash(NODE3) = KEY3;

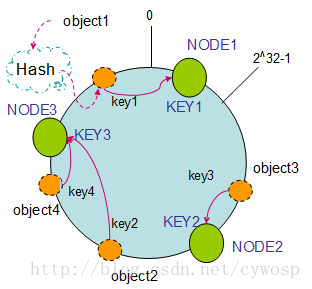
通过上图可以看出对象与机器处于同一哈希空间中，这样按顺时针转动object1存储到了NODE1中，object3存储到了NODE2中，object2、object4存储到了NODE3中。在这样的部署环境中，hash环是不会变更的，因此，通过算出对象的hash值就能快速的定位到对应的机器中，这样就能找到对象真正的存储位置了。

机器的删除与添加

普通hash求余算法最为不妥的地方就是在有机器的添加或者删除之后会照成大量的对象存储位置失效，这样就大大的不满足单调性了。下面来分析一下一致性哈希算法是如何处理的。

节点（机器）的删除

以上面的分布为例，如果NODE2出现故障被删除了，那么按照顺时针迁移的方法，object3将会被迁移到NODE3中，这样仅仅是object3的映射位置发生了变化，其它的对象没有任何的改动。如下图：

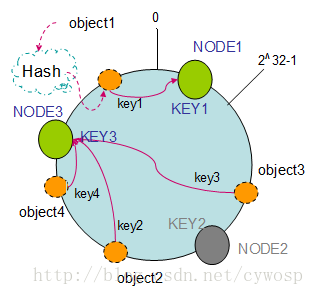
节点（机器）的添加

如果往集群中添加一个新的节点NODE4，通过对应的哈希算法得到KEY4，并映射到环中，如下图：

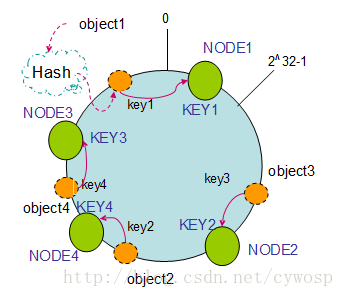
通过按顺时针迁移的规则，那么object2被迁移到了NODE4中，其它对象还保持这原有的存储位置。通过对节点的添加和删除的分析，一致性哈希算法在保持了单调性的同时，还是数据的迁移达到了最小，这样的算法对分布式集群来说是非常合适的，避免了大量数据迁移，减小了服务器的的压力。

平衡性

根据上面的图解分析，一致性哈希算法满足了单调性和负载均衡的特性以及一般hash算法的分散性，但这还并不能当做其被广泛应用的原由，因为还缺少了平衡性。下面将分析一致性哈希算法是如何满足平衡性的。hash算法是不保证平衡的，如上面只部署了NODE1和NODE3的情况（NODE2被删除的图），object1存储到了NODE1中，而object2、object3、object4都存储到了NODE3中，这样就照成了非常不平衡的状态。在一致性哈希算法中，为了尽可能的满足平衡性，其引入了虚拟节点。

以上面只部署了NODE1和NODE3的情况（NODE2被删除的图）为例，之前的对象在机器上的分布很不均衡，现在我们以2个副本（复制个数）为例，这样整个hash环中就存在了4个虚拟节点，最后对象映射的关系图如下：

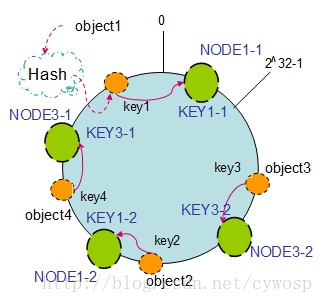
根据上图可知对象的映射关系：object1->NODE1-1，object2->NODE1-2，object3->NODE3-2，object4->NODE3-1。通过虚拟节点的引入，对象的分布就比较均衡了。那么在实际操作中，正真的对象查询是如何工作的呢？对象从hash到虚拟节点到实际节点的转换如下图：

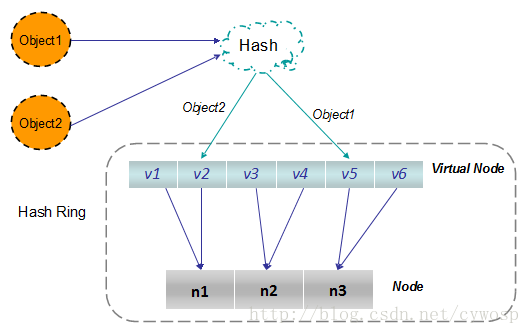
“虚拟节点”的hash计算可以采用对应节点的IP地址加数字后缀的方式。例如假设NODE1的IP地址为192.168.1.100。引入“虚拟节点”前，计算 cache A 的 hash 值：

Hash(“192.168.1.100”);

引入“虚拟节点”后，计算“虚拟节”点NODE1-1和NODE1-2的hash值：

Hash(“192.168.1.100#1”); // NODE1-1

Hash(“192.168.1.100#2”); // NODE1-2

重要结论

这篇文章中从理论上证明了几个重要的结论：

定论4.1 上面文章中描述的ranged hash family是满足上面所要求的4个属性的；

定论4.3 Every monotone ranged hash function is a 派-hash function and vice versa

一个派hash函数就是跟排列相关的函数，而Maglev hash正是此类函数簇的一个实现。

参考

All content is licensed under CC BY-NC-SA

Buit with Jekyll and 3-Jekyll theme • Hosted on Github

Table of Contents