2017 May 10

关于并发控制的乐观方法

论文题目: On Optimistic Control Methods for Concurrency Control

本论文发表之时，数据库系统中并发控制最常见的方法是对数据对象加锁。本论文提出了乐观方法＋事务备份(transaction backup)进行并发控制，以期望达到最理想的状态，即事务之间的冲突不再发生。

1. 介绍

本论文发表于1981年。作者是H.T.KUNG和JOHN T.ROBINSON, Carnegie-Mellon University(卡内基梅隆大学)。第一个作者简介可以看 https://en.wikipedia.org/wiki/H._T._Kung ，是个中国人，孔祥重，主要研究领域是机器学习，信号处理，并行计算等。

1.1 数据库和事务

数据库是什么？
1. 数据库是对象的集合,对数据库的共享访问就是对这些对象的访问;
2. 对象分为两类: roots, 它们是一些distinguished objects; 其他对象,必须先访问roots,然后通过指向这些对象的指针来访问;
事务是什么？
1. 对数据库中的对象的一系列访问的集合;
2. 保证访问数据的完整性约束;

如果我们的目标是最大化数据库访问的吞吐量，那么就至少以下两种用例希望达到这个目标：

数据量巨大，在任何一个时刻只有数据库的小片数据出现在主存中；所以需要从辅存上交换数据库的另外部分；
即使整个数据库可以放在主存中，也会存在多进程的访问；

也正因如此，才需要一个好的并发控制方法，以能够最大化地使用底层地硬件资源。

1.2 锁并发控制

现有加锁方法来控制并发的缺点:

锁的管理负荷。
- 即使是只读事务也要加锁;
- 死锁检测的负载;
no general-purpose deadlock-free locking protocols(没有一个普世的无死锁协议存在)。
- 投入了大量研究来发展专门目的的锁协议；
- 举例：B-Tree索引在其他论文中有9种加锁协议;
对象加锁后,等待磁盘访问的过程中,降低了访问的并发度;
不得已回滚事务时,必须要到事务结束时才能释放所有锁,这也降低了访问的并发度;
加锁应该是在最坏的情况下的选择,而不应该是一种常态;

2. 无锁机制

前提条件

在给定时刻,数据库中的对象要比运行中的事务所涉及的对象数目要多得多;
运行中的事务同时修改数据库中的同一对象的概率要小得多;

以上 2 点主要说明事务模型的冲突是不常见的

主要优点

事务冲突很少见;
本协议具有普遍性;
无死锁发生;

主要想法

读是不受限制的,主要指从一个节点读取其值或指针;但是,一个查询的结果返回认为是一个写操作,需要进行校验;
写是严格受限的。事务主要由 读阶段、校验阶段、写阶段(可选) 这 2/3 个阶段构成。

主要阶段

读阶段:所有的写操作发生在局部的、节点副本上,只在事务内可见;
校验阶段: 用来保证数据完整性
写阶段: 校验成功后才存在,主要是让修改完成的数据全局可见;

如果事务发生失败,需要把事务进行备份,然后再次调用重新执行。

2.1 读和写阶段

我们假定由底层系统来提供对象的管理，主要的操作有

Create 创建一个新对象并返回其名字
delete(n) 删除对象 n
read(n, i) 读取对象 n 的项 i 并返回其值
write(n, i, v) 写入对象 n 的项 i 的值 v
copy(n) 创建对象 n 的副本并返回其名字
exchange(n1, n2) 交换两个对象 n1 和 n2 的名字

其中 n 是对象的名字, i 是类型管理的一个参数, v 是类型的值(可能是指针,可能是数据)

事务使用如下进行操作。

tcreate = (
    n := create;
    create set := create set U { n } ;
    return n
)

twrite(n, i, u) = (
    if n E create set
        then write(n, i, u)
    else if n E write set
        then write(copies[n], i, u)
    else (
        m := copy(n);
        copies[n] := m;
        write set := write set U {n};
        write (copies[n], i, u)
    )
)

tread(n, i) = (
    read set := read set U {n} ;
    if n E write set then
        return read (copies[ n], i)
    else
        return read (n, i)
)

tdelete (n) = (
    delete set := delete set U { n }
)

对于每一个事务，并发控制会维护着该事务需要访问的对象的集合。一开始，tbegin调用会初始化该集合为空。
用户写的事务执行，就是上面所提及的读阶段；
用户写的tend才会触发上面所提及的校验阶段和写阶段；
copies是对象名字映射的向量。
读阶段并不会发生全局写。对对象的第一次写，会复制一个副本，后面所有的写将会对这个对象副本进行。副本在读阶段过程中对其他事务是不可见的。

另外，我们约定：（1）所有的节点都是通过root节点的指针来访问的；而所有事务都知道root节点的全局名字。那么，root节点的副本是无法访问的，因为它不在全局名字集合之内。（2）root节点是不会创建和删除的，节点删除后不会留下dangling pointer，创建的节点通过新建立的指针变得可访问；

事务完成之后，就会使用tend来调用校验过程。只有校验成功之后，才会进入到写阶段：

for n E write set do exchange(n, copies[n]).

写阶段完成之后，事务创建的所有节点将全局可见，事务删除掉的节点将全局不可再见。事务无论成功还是失败完成之后，将会进行一定的清理工作：

(for n E delete set do delete(n);
 for n E write  set do delete(copies[n])).

2.2 校验阶段

假定T₁,T₂,…,T_n是并发执行的。这些事务操作的共享数据结构是d，而D是所有d的完整集合，那么事务T_i就是这样的一个函数：

T_i: D → D.

假定初始化的数据结构是d_init，而最终的数据结构是d_final。那么事务过程就可以看成是将一个并发事务的排列的函数组合应用于数据结构的结果(其中，排列是用派表示，组合是用小圈圈表示)，即：

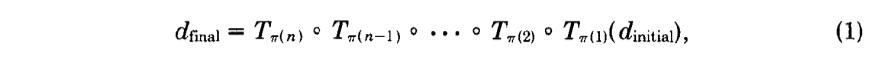
上面这个公式可以使用归纳法证明是成立的，只要每一步满足数据完整性，那么整个操作序列就可以保证数据的完整性。而这一公式也正是(validation of serial equivalence)等同于序列化的检验成功的条件。那么，关键的问题就是找到这样的一个事务排列。

在事务执行过程中，显式地给每一个事务赋于一个唯一的事务号t(i)，也就是说，无论何时，下面描述都要成立，以保证serially equivalent schedule。

只要时间t(i) < t(j)成立时，事务T_i一定比事务T_j来的早

原文如下：

there must exist a serially equivalent schedule in which transaction T_i comes before transaction T_j whenever t(i) < t(j).

要保证这一点的成立，这个排列中的两个事务需要满足下面的三个要求之一；

条件一

T_i completes its write phase before T_j starts its read phase

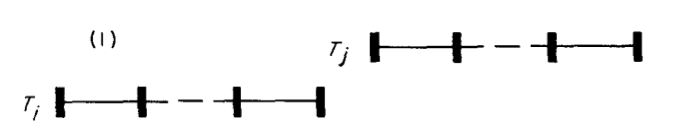
条件1说明，事务T_i先完成，然后事务T_j才开始；很明显，如果两个事务的执行时间段是没有交集的，必然可以保证数据的完整性。

条件二

The write set of T_i does not intersect the read set of T_j , and T_i completes its write phase before T_j starts its write phase.

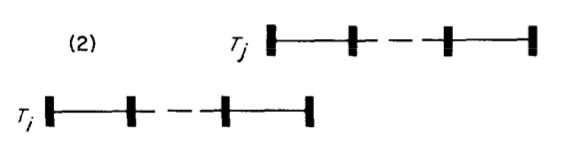
条件2说明，事务T_i的写阶段不会影响到事务T_j的读阶段，事务T_i完成了其写阶段之后事务T_j才开始写阶段，所以事务T_i不会覆盖写事务T_j；（同样，事务T_j不能够影响T_i的写阶段）

条件三

The write set of T_i does not intersect the read set or the write set of T_j, and T_i completes its read phase before T_j completes its read phase.

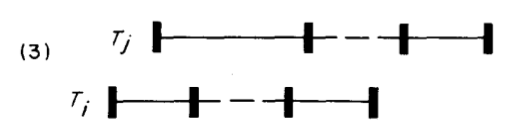
条件3跟条件2类似，只是简单要求事务T_i不会影响事务T_j的读阶段或者写阶段；同样，事务T_j不能够影响事务T_i的读阶段；

2.2.1 赋于事务号

事务号使用连续递增的数字
在何时赋于事务号？
- 方案1：在读阶段之前赋值（有缺陷，见下图）
- 方案2：在读阶段结束时赋值

方案1存在的缺陷

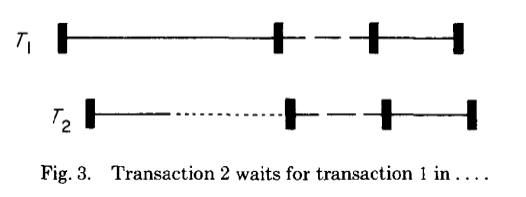
T₂读阶段早结束于T₁读阶段（时长大），但是可能不得不等待T₁读阶段的结束。

2.2.2 实践性问题

考虑这样的一个问题，事务T有一个较长的读阶段。那么当事务T进行校验时，哪些事务的写集合是要进行检查的？

在T之前完成了它们的读阶段，并且
T开始时还尚未完成它们的写阶段

但是并发控制只能够管理有限的写集合，这样就有一个困难：如果这样的事务是普遍的，上述事务号的赋值方法是不合适的。还好，这种情况是不常见的；但是我们仍然是需要解决这个问题的。

当事务T进行校验时，必须检查T₁的写集合。

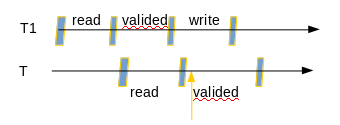
为此，并发控制协议需要维护一个有限的most recent write sets，其大小要足够大以校验几乎所有的事务。写集a比写集b more recent 是指对应的事务号保持大于关系。

如果写集校验失败的话，那么，事务T校验失败，需要对它进行备份; 然后，给它一个新的事务号，进行重新调度。这样就存在这样的一个问题：失败的事务会重复地失败，造成一个饿死现象。对于此问题的解法是，一旦监测到事务饿死的问题，就让它在tend时进入一个临界区，不释放任何semaphore的情况下重新开始执行，以保证其成功完成。这相当于对整个数据库加了一个写锁保护；好在，这样的问题是非常非常少见的。

下面讨论校验阶段的优化，主要考虑的是前2个条件，这就要求事务的写阶段需要串行化地执行起来。

2.3 串行校验

最简单方案是：事务号赋值、校验阶段和写阶段，全部都放在临界区内。临界区在下面使用< > 来表示。

tbegin = (
    create set := empty;
    read set := empty;
    write set := empty;
    delete set := empty;
    start tn := tnc
)

tend = (
    < 
    finish tn := tnc;
    valid := true;
    for t from start tn + 1 to finish tn do
        if (write set of transaction with transaction number t intersects read set)
            then valid := false;
    if valid
        then ((write phase); tnc := tnc + 1; tn := tnc)
    >
    if valid
        then ( cleanup )
    else (backup)
)

上面已有优化：只有在校验成功时，才会消耗1个事务号；

如果涉及到多CPU时，就需要将校验阶段的步骤进行并行化，下图中的优化点主要是：

读阶段完时，读取tnc并将其它赋给mid tn。很明显，事务开始时的事务start tn+1, start tn+2,…,mid tn的写集合是需要校验的，并且可以在临界区外进行校验；

tend := (
    mid tn := tnc;
    valid := true;
    for t from start tn + 1 to mid tn do
        if (write set of transaction with transaction number t intersects read set)
            then valid := false;
    <
    finish tn := tnc;
    for t from mid tn + 1 to finish tn do
        if (write set of transaction with transaction number t intersects read set)
            then valid := false;
    if valid
        then ( (writephase); tnc := tnc + 1; tn := tnc)
    >
    if valid
        then (cleanup)
    else (backup)
)

同样，还可以再进行一次优化。就是再读一次tnc作为finish tn，然后将mid tn到finish tn之间的写集进行校验。重复这个过程，我们就可以把校验阶段分为多个小步，然后这些小步就可以并行化。可以看出，整体的思想就是：

将变化的部分移出临界区之外，增加并行度

目前为止，我们的讨论还不涉及只读事务的问题，或者说查询。因为查询是没有写阶段的，没必要给它们一个事务号；只需要在读阶段末尾时读取tnc，并把它赋给finish tn; 查询的校验包括了检查 start tn+1, start tn+2,…, finish tn之间事务的写集合。并且这不需要放在临界区内，这一点对于下文的讨论也是成立的。

2.4 并行校验

tend = (
    <
    finish tn := tnc;
    finish active := (make a copy of active)
    active := active U { id of this transaction }
    >
    valid := true;
    for t from start tn+1 to finish tn do
        if (write set of transaction with transaction number t intersects read set)
            then valid := false;
    for i E finish active do
        if (write set of transaction Ti intersects read set or write set)
            then valid := false;
    if valid
        then (
            (write phase);
            <
            tnc := tnc + 1;
            tn := tnc;
            active := active -- (id of this transaction) 
            >
            (cleanup)
        )
        else (
            <
            active := active -- { id of transaction } 
            >
            (backup)
        )
)

3. 分析一个应用

主要是针对B-tree索引的并发插入进行分析。

首先要考虑的是读集和写集的大小，其期望值应该是多大；这直接影响了校验阶段所花费的时间。btree页作为写集和读集的单元
还要再考虑的是完成校验＋写阶段的总时间与完成读阶段时间的比较。

后面的分析主要是公式性地推导和说明，并没有实验测试和数据支持，所以不再简述。

4. 总结

本论文主要提出并发控制的两个机制：乐观并发；事务备份。主要适用的场景是事务冲突非常少的场景，像查询为主的系统和非常大的树结构索引。

我的总结

据我所知，使用OCC方法的数据库系统是比较少的。这种方法非常适用于AP以查询为主的系统。